「量子コンピュータ」はどうやって動いているのか? プログラミングはどのようなものか?
テクノロジーのニュースで量子コンピュータという言葉を耳にする機会が多くなってきました。量子コンピュータの最初の概念は、1982年に物理学者であるリチャード・ファインマンによって提唱されました。
当時は量子力学を利用した計算機の可能性について考察されたものですが、近年は実際にハードウェアである量子ビットからなる量子コンピュータが登場し、大きな注目を集めています。IBMやGoogle、Intelなどの大手テクノロジー企業や、新興の量子コンピューティング企業が、量子ビットを用いた量子コンピュータの開発に取り組んでいます。これらの量子コンピュータは、従来の古典的なコンピュータとは異なる原理を基盤としており、量子の重ね合わせや量子もつれといった特性を利用して計算を行います。量子コンピュータは、特に複雑な問題や量子化学、暗号解読などの分野で従来のコンピュータよりも高速で効率的な計算を可能にすると期待されています。
本記事では量子コンピュータを少しでも分かっていただけるよう紹介します。コンピュータという単語がついているのでなんとなくわかるようでわからないもやもや感を持っている皆さんも多いかと思います。
今のスーパーコンピュータでも解けない問題でも解けるとはどういうことなのか、簡単な問題例と簡単な量子プログラムも載せていますので興味あるかたは参考にしてください。量子プログラムのコード部分を読み飛ばしてプログラミング例として見て頂いて構いません。
量子コンピュータのハード構造
皆さんがよく目にする巨大な円筒形の装置それが量子コンピュータです。
真空管デバイスのENIACの巨大な計算機から量子コンピュータまでステップアップするのに74年経っています。これを長いとみるか短いとみるか。電子の制御状態を利用した従来のコンピュータから量子の挙動を利用したコンピュータが出来上がるまで100年も経っていません。当時の開発者からは想像もできなかったことでしょう。
では現在のコンピュータの頭脳CPUにあたる計算機はどこに収まっているのでしょうか?巨大な円筒形の金色の構造物の大部分は冷却器であってその先端に量子ビットの素子が入ったチップが収まっています。
超伝導量子ビットチップは数㎜角の大きさでその中には数量子ビットから数百量子ビットの素子が格子状に入っています。量子ビットの素子の格子状の配置構造は量子ハードウェア開発企業googleやIBMによって独自の構造をしています。
| 超伝導量子ビット | 数ミリメートル角 |
| トラップ型イオン量子ビット | 数マイクロメートル |
| 量子ドット量子ビット | 数百ナノメートル |
| 窒素空孔量子ビット | 数ナノメートル |
量子ビットの種類により数ナノメートルから数ミリメートルまでありますが、ここでは主に超伝導量子ビットについて紹介していきます。
円筒形内部の冷却構造 (EPJ Quantum Technology volume 6, Article number: 2 2019より)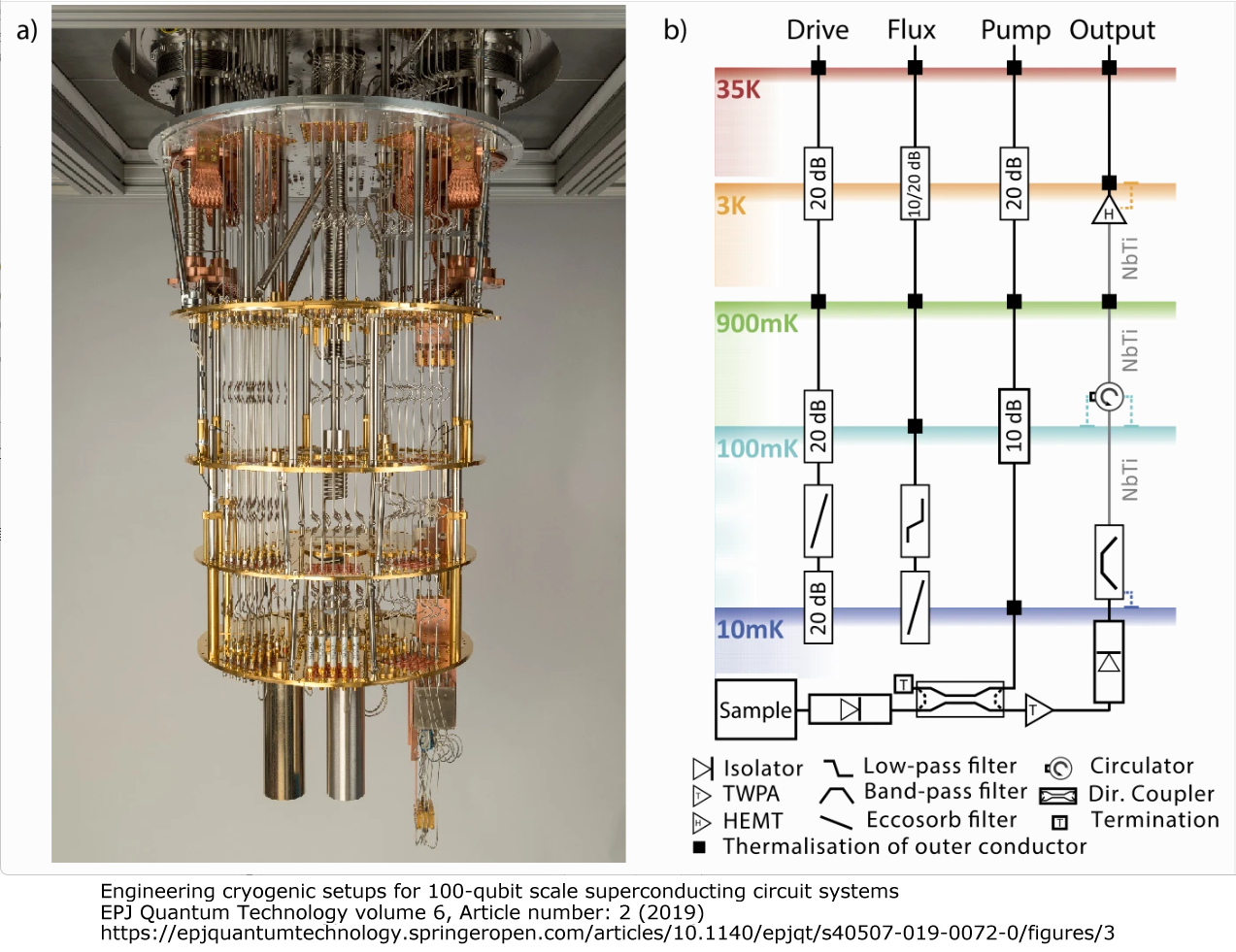
最下部に超伝導量子ビットチップが納めされており10mK(=0.01K) でおよそ-273℃に冷却され超電導状態にあります。超高速計算を実現するためには、粒子同士が分離された状態(重ね合わせの状態)を保持する必要があります。
そのために、外部環境などの「ノイズ」を限りなく除去する必要があり、1K(ケルビン)レベルの極低温環境を作る必要があるからです。量子ビットのチップを超電導状態にする必要があるので、装置が大きくなるのです。
IBMの量子コンピュータの内部構造(IBM Access quantum computingのページより)
IBMの量子コンピュータも同じような構造をしています。最下部の弁当箱のようなものに量子ビットチップが納めされています。
量子ビットの他に重要な構成要素として量子ゲートがあります。これは現在のコンピュータの論理ゲートの量子版として、量子コンピュータではそれぞれ論理ゲートがあります。
論理ゲートの組み合わせで表現される論理回路に対応するものに量子回路がありこれは量子アルゴリズムとも呼ばれます。
量子ビット
量子ビット(qubit)は、量子コンピュータの根本であり、量子情報処理において情報の基本単位です。量子コンピュータは0,1と重ね合わせ状態があります。
現在のコンピュータの0,1のビットからその動作は似て非なるもので、0,1と述べましたが、これは数字でいうところの0,1ではなくて正しくはベクトルの方向によります。量子コンピュータはもはや0,1の数値の世界ではなくて、「複素ベクトル」を理解できるというものです。「複素ベクトル」という言葉が出てきましたが、高校数学で習うベクトルと複素数を組み合わせたものです。ここでは量子力学では必須のものと知るだけでかまいません。ベクトルという名がついているとおり、量子ビットは矢印の方向で表せます。
量子ビットを視覚化したブロッホ球
量子ビットを3次元球上で視覚化したものにブロッホ球(Bloch ball)があります。1量子ビットの状態を半径1の単位球面上の点として表したモデルです。0↑(上向)、1↓(下向)を基本状態とし、上向きでも下向でもない←→の状態である重ね合わせ状態のいずれかになります。量子コンピュータの演算はこの矢印を回してその結果を得るものです。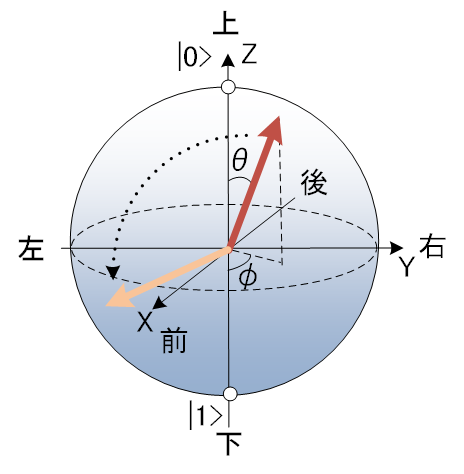
0、1と書くと通常のコンピュータと同じですが、量子コンピュータはそれぞれ次のような表記をします。量子コンピュータのビットは|0>、|1>のようにケット記号と呼ばれる特殊な括弧の記号を使って表現されます。これは古典ビットの0、1とは違い、いわゆる量子状態にラベルをつけたものです。
量子ビットの表現
|0> 上向、|1> 下向、|0> + |1> 重ね合わせ状態で表せます。
重ね合わせ状態も←←、→→、→←、←→というような状態もあり、このような量子ビットが持つ状態を制御可能な量子ゲートが存在します。
量子ゲートはいろんな論理タイプのものが存在します。ただしそのタイプごとにハードウェアがあるのではなくて、超伝導量子ゲートの場合は、その制御操作において高周波パルス(マイクロ波)の投入となり、反射結果を観測することで、量子ビットの状態を観測します。
他の量子ビットの種類として、トラップ型イオン量子ビット:レーザー光を用いて量子ビットの状態を制御するものや、量子ドット量子ビット:電磁波や磁場を用いて量子ビットの状態を制御するものもあります。
複数の量子ゲートを接続することによって量子回路を作ります。量子回路といっても物理的な線が存在するわけではなくて、高周波パルス(マイクロ波)の投入、結果を繰り返す操作そのものです。これが量子アルゴリズムと呼ばれます。
量子コンピュータの演算は視覚的にはブロッホ球上の矢印を回してその結果を得るものです。
量子ゲートと量子演算
量子ゲートを利用して量子演算をするわけですが、各量子ゲートの真理値表が分かれば、それを使って回路を構築し計算することができます。
1ビットの量子演算
今のコンピュータの論理演算は簡単です。それこそ小学生でも理解ができるほどです。
1ビット演算はNOTの1種類だけです。NOTは単一の入力を受け取り、その入力を反転します。1ビットの量子演算では多数の種類の演算がありますが、よく使われる演算はつぎのようなものです。
Xゲート(パウリXゲート)
これは古典コンピュータでいうところのNOTゲートに相当します。Xゲートは量子ビットの状態を反転させます。
真理値表
| 入力 | 出力 |
| |0> | |1> |
| |1> | |0> |
| |0>+|1> | |1>+|0> |
上表で|0>+|1>と|1>+|0>は量子計算の観点から同じ状態です。XゲートがあればY,Zゲートというものもあります。
Hゲート(アダマールゲート)
これは、量子ビットを重ね合わせ状態にします。具体的には、|0> 状態を(|0> + |1>)/√2の重ね合わせ状態に、|1> 状態を (|0> - |1>)/√2の重ね合わせ状態に変換します。
真理値表
| 入力 | 出力 |
| |0> | |0>+|1> |
| |1> | |0>-|1> |
| |0>+|1> | |0> |
|0>+|1>は重ね合わせを表現していましたが、|0>-|1>はどうなのでしょうか? 同じく重ね合わせ状態ですが、|0>と|1>の間で位相差を持つ状態です。このような結果の状態がどのような計算に特があるのかは、次章以降で述べます。
Sゲート
これは、位相ゲートとも呼ばれます。Sゲートは、|1> 状態の位相を90度(π/2)回転させます。位相ゲートでTゲートと呼ばれるものもあります。
1ビットの量子演算だけでも複数存在し、場合によっては独自の位相ゲートも定義できます。前にも述べたように、量子ゲートの操作は高周波パルス(マイクロ波)の投入であり、自由にその波の種類は定義できます。独自の位相ゲートを定義することで、任意の位相の変更が可能になります。これは量子アルゴリズムや量子回路の設計において重要な役割を果たします。
2ビットの量子演算
2ビットとなると更に演算の種類が今のコンピュータより多くなります。組みあわせるだけで今のコンピュータをはるかに凌ぐことが予想できます。
CNOTゲート
2ビット量子演算で一番有名なのが、CNOTゲートです。コントロールNOTと呼ばれるもので、1番目の量子ビットの状態を見て2番目の状態の量子ビットの状態をNOTにするかどうか決定するもので、コントロール(制御)するということでこの名がついています。
真理値表
| 入力A | 入力B | 出力A | 出力B |
| |0> | |0> | |0> | |0> |
| |1> | |0> | |1> | |1> |
| |0> | |1> | |0> | |1> |
| |1> | |1> | |1> | |0> |
この表をみると出力BはXORの論理演算と類似しています。では、Aに|0>+|1>、Bに|0>を入力するとどうでしょうか?
2量子ビットの状態は|00>+|10> つまり、Aは|0>+|1>、Bは|0>です。
この状態の量子演算に意味があるのかないのか、わけがわからないですが、それでいいのです。1+1は2というような感じで受け止めておきましょう。この量子状態というものに量子力学の不思議が凝縮されています。
1つの量子ビットは、例えば1/√2|0>+1/√2|1>といった、|0>と|1>が同じ確率で重なり合った状態をとります。
これが先に述べた“中間的”という意味です。ただし、重なり合った状態が保たれるのは、誰も見ていない状態に限り、その状態を観測すると50%の確率で|0>に、50%の確率で|1>になります。量子力学では、これを測定による状態の収縮と言いますが、これが量子計算にとって重要な要素になります。
量子アルゴリズムとは
量子演算の真理値表が定義されれば、それを使って量子アルゴリズムを書くことができます。
前の章で量子演算の主なゲートを真理値表とともに見てきましたが、これらのゲートを組み合わせて、課題となる事象に対してアルゴリズムを作り結果の出力を得ることが目的です。量子アルゴリズムと呼ばれます。
ソフトウェア―技術者は量子コンピュータのハード部分の量子ビットチップを研究する物理学者、材料物性学者のように量子力学を意識する必要はありません。量子アルゴリズムに専念すればいいのです。
量子アルゴリズムをプログラムで表現する場合はどのようなものでしょうか? ここで一例をあげておきます。ここでは、内容の理解よりもプログラミングがどのように行われるのかを見て頂ければと思います。
量子コンピュータのシミュレーションフレームワーク(Qiskit)を使用します。Qiskitは、IBMが提供する量子コンピューティングのためのオープンソースのソフトウェア開発フレームワークです。
では、PythonとQiskitを使用して一番簡単なベルシュタインとヴァジラニの問題を解いてみましょう。
ベルシュタイン-ヴァジラニのアルゴリズムは、2つの量子ビットを使用して、2つの関数が一致するかどうかを判定する問題です。
問題:”数当てゲーム”
箱の中に0か1の数字が書かれたボールが並んで2個入っています。
この箱は0か1のいずれかの数字を順に入口に入れると、出口から順に正解であれば1、不正解であれば0と教えてくれます。確実に正解を分かるには何回の試行をすればいいでしょうか?
答えは2回です。10、01を投入して結果から判断します。各ボールの1、0を順番に判定するのです。
量子コンピュータであれば答えは1回です。たいしたことないじゃないかと思われますが、これが100個だろうが1,000個だろうが試行はたった1回で済むのです。(ただし1,000個の場合は量子ビットが1,000個必要で、ずいぶん贅沢な使い方になります)
”数当てゲーム”をQiskitで量子プログラムしてみましょう!
import numpy as np
from qiskit import QuantumCircuit, QuantumRegister, ClassicalRegister, execute
def bernstein_vazirani(n: int) -> int:
"""
ベルシュタイン-ヴァジラニ問題を量子アルゴリズムで解く
Args:
n: 問題のサイズ
Returns:
正解の数字 (00,01,10,11)
"""
# 量子レジスタと古典レジスタを準備
qr = QuantumRegister(n + 1)
cr = ClassicalRegister(n)
qc = QuantumCircuit(qr, cr)
# 初期状態
qc.initialize(np.array([1, 0], dtype=complex), qr[0])
for i in range(1, n + 1):
qc.h(qr[i])
# オラクル演算
for i in range(n):
qc.cx(qr[0], qr[i + 1])
# 測定
for i in range(n):
qc.measure(qr[i + 1], cr[i])
# シミュレーションを実行
job = execute(qc, backend="local_simulator")
result = job.result().get_counts()
# 最も頻度の高い測定結果を返す
max_count = 0
max_key = 0
for key, count in result.items():
if count > max_count:
max_count = count
max_key = key
return int(max_key[0])
# 問題のサイズ
n = 3
# 問題を解く
answer = bernstein_vazirani(n)
# シミュレーションを実行
job = execute(qc, backend="local_simulator")
result = job.result().get_counts()
# 各組み合わせの出現頻度を表示
for key, count in result.items():
print(f"{key}: {count}")
# 正解を表示
print(f"正解は {answer} です")
qc.h はアダマールゲート(Hゲート)
qc.cxはコントロールNOT(CNOTゲート)
01: 2
10: 1
11: 0
正解は 00 です
シミュレーションですので今回仮定で用意されたボールは00で、箱の中の00を当てたことになります。このプログラムは100個でも使えます。100個の数字を判定するには100+1個の量子ビットが必要です。(シミュレーションでは実行毎に仮定で用意されたボールは変わりますので都度答えも変わります)
このような単純な問題に現実の量子コンピュータで100+1個の量子ビットを使うのは贅沢すぎますが。
ここまで上げたプログラムはあくまでシミュレータです。本物の物理的な量子コンピュータでは、量子回路の構築、量子オラクルの構築では、物理的に量子ゲートを組み合わせて回路を作成することになります。今のCPUボードの回路を作るようなものです。ただしこの専用の量子回路を作ってしまうとそれ専用の働きしかしないので、汎用の量子コンピュータが必要となってきます。
汎用の量子コンピュータとは
汎用の量子コンピュータは、様々な問題を解決するために設計された量子計算機です。汎用の量子コンピュータは、古典的なコンピュータと同様に、さまざまなアルゴリズムやアプリケーションを実行できるように設計されています。これは、量子ビットを使用して情報を処理し、量子ゲートを適用して計算を行います。
汎用の量子コンピュータは、古典的なコンピュータと同様に、プログラミング可能であり、さまざまなアルゴリズムや問題に対応できます。これらのアルゴリズムは、量子ビットと量子ゲートを操作することによって実装され、量子コンピュータ上で実行されます。
汎用量子コンピュータでは、「量子アルゴリズムとは」で上げたプログラムも含めて同じような手法でプログラミングできます。ただし実際の量子コンピュータ上で実行する際には、いくつかの注意点があります。例えば、量子ビットのエラー率やゲートの精度、量子ビット間の結合強度など、ハードウェアの物理的な制約を考慮する必要があります。また、量子ビットの初期化や測定に関する手順も異なる場合があります。
以下、汎用の量子コンピュータ上で実行可能なプログラミングの一例として挙げておきます。前回同様IBMのQiskitを使用して、量子ビットを用いた量子回路を構築し、実行するPythonのコード例を示します。前述の問題:”数当てゲーム”をもっと効率的に解決する方法があります。
例えば、グローバーの量子探索アルゴリズムを使用することで、量子ビットの数を最小限に抑えながらも解を見つけることができます。
”数当てゲーム”をグローバーの量子探索アルゴリズムで書く
from qiskit import QuantumCircuit, Aer, execute
def grover_search(oracle):
"""
Grover探索アルゴリズム
Args:
oracle: オラクル演算
Returns:
測定結果
"""
# 量子回路を作成
qc = QuantumCircuit(2)
# 初期化
qc.h(0)
qc.h(1)
# オラクル演算
oracle(qc)
# Grover拡散演算
for _ in range(int(numpy.sqrt(4))):
qc.h(0)
qc.h(1)
qc.cx(0, 1)
qc.x(1)
qc.cx(0, 1)
qc.h(0)
qc.h(1)
# 測定
qc.m(0)
qc.m(1)
# シミュレータで実行
simulator = Aer.get_backend("aer_simulator")
job = execute(qc, simulator, shots=100)
# 測定結果を取得
counts = job.result().get_counts()
return counts
# オラクル演算を定義
def oracle(qc):
# ここに、探索対象のデータベースに基づいたオラクル演算を記述
# 例:
qc.cx(0, 1) # 解である状態のみ状態を反転
# 実行
counts = grover_search(oracle)
# 結果を出力
print(counts)
グローバーの量子探索アルゴリズムの量子回路をブロック図で描くと
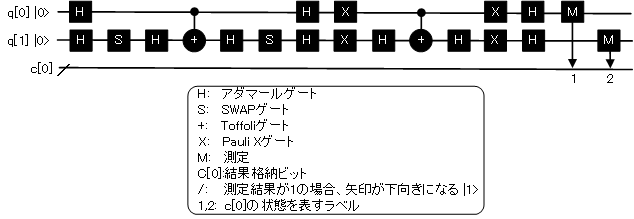
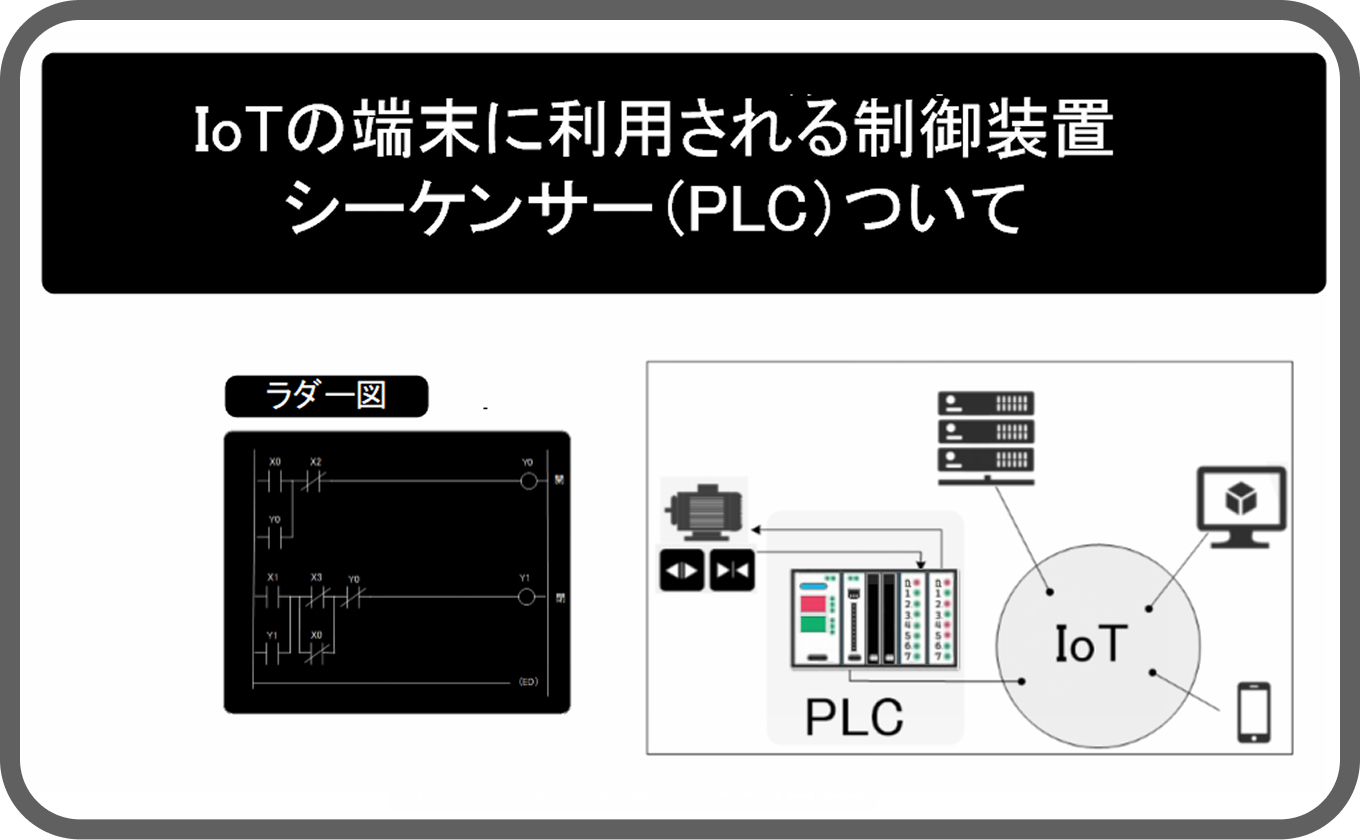
q[0]、q[1]は量子ビットで2ビット使っています。こちらの方がブロック図ですのでプログラムコードよりは見やすいかもしれませんが、これだけを見てグローバーの量子探索アルゴリズムを表現しており、理解できるかというと筆者にも分かりません。筆者が過去にやってきたシーケンサーのラダー図を書いているような錯覚におちます。ずっと未来には手のひらにのる量子シーケンサーなるものが出来ているかもしれません。
https://www.value-domain.com/media/plc/
このプログラムは、Groverのアルゴリズムを使用して与えられた論理式を解析し、正しい解を見つけます。量子ビットの数が増えても、Groverのアルゴリズムは比較的効率的に動作し、古典的なアルゴリズムよりも高速に解を見つけることができます。
このようなアルゴリズムを実装することで実際の汎用量子コンピュータを動かすことができます。
量子プログラミング言語自体は簡単ですが、問題解決をするための記述を発想することが今のところ難しいところで、このあたりはAIの進化でより簡単に問題解決のためのスクリプト言語ができたらと思います。
余談になりますが、シミュレーションで動作させる量子アルゴリズムはあくまで現在のコンピュータがシミュレートしています。そのため量子ビット数を増やして複雑な計算を並列処理させると当然計算時間も大幅に増えます。この量子シミュレータの量子回路計算を200倍速くする技術を2024年2月19日に富士通が発表しました。
https://pr.fujitsu.com/jp/news/2024/02/19.html
量子コンピュータの計算はそんなに早いのか
前章でプログラミングの専門的な話になりましたが、プログラミングの例の中で量子回路中の量子ビット数を2や3にしましたが、量子ビット数をもっと増やせば並列処理できる数も増加し複雑な問題も素早く解けるようになります。
並列処理なら今のコンピュータもCPU、MPUを複数実装してできるではないかと思われますが、量子コンピュータの並列処理はそれとは趣が違います。量子コンピュータと従来のコンピュータの並列処理にはいくつかの重要な違いがあります。
以下の主な3つの重要な違い。
基本単位の違い
従来のコンピュータでは、CPUやGPUなどのプロセッサが基本的な処理単位です。これらのプロセッサは複数のコアを持つことができます、それぞれが異なるタスクを並列に処理することができます。
一方、量子コンピュータでは、基本的な処理単位は量子ビット(qubit)です。量子ビットは従来のビットとは異なり、量子力学の原理に従って状態を並列に処理することができます。
並列度の違い
従来のコンピュータでは、並列処理は通常、複数のプロセスやスレッドを使用して行われます。これにより、複数のタスクを同時に処理することができますが、物理的な制約により、ある程度までしかスケールしません。
量子コンピュータでは、量子ビットの性質により、非常に高度な並列処理が可能です。量子ビットが重ね合わされた状態(重ね合わせ状態)にある場合、全ての状態を同時に処理できます。これにより、指数的な数の状態を一度に扱うことができ、従来のコンピュータよりもはるかに高速に問題を解決することができます。
同期性の違い
従来のコンピュータの並列処理では、プロセスやスレッド間の同期が重要です。データの競合を避けるために、適切な同期機構を使用する必要があります。
一方、量子コンピュータでは、量子ビットが重ね合わされた状態にある場合、同期性の概念が異なります。
量子アルゴリズムは、重ね合わせ状態のまま並列な操作を行うことができますが、従来の同期処理のような機構は必要ありません。
これらの違いにより、量子コンピュータは特定の問題においては従来のコンピュータよりも効率的であり、特に量子アルゴリズムが問題の解決に役立つ場合があります。しかし、量子コンピューティングの実現にはまだ多くの技術的課題が残されており、一般的な利用には時間がかかると考えられています。
「グーグルは2019年、53個の量子ビットを使い、最先端のスーパーコンピュータで約1万年かかる計算を約3分で解いた」と発表しましたが、これは53量子ビットの量子コンピュータ「Sycamore」を使用して、ランダムな回路をシミュレートするタスクを実行しました。このタスクは、ランダムな量子ビットの状態を生成し、その状態を特定の基準で測定するというものでした。
Googleの量子コンピュータはこのタスクを約3分で完了しましたが、同様のタスクを実行するのに、当時の最先端のクラシックスーパーコンピュータである「Summit」などの計算機には、約10,000年かかると推定されていました。
量子コンピュータの得意計算の分野は?
量子コンピュータの計算は全てが早いというわけではなく得意な領域においてのみ今のコンピュータよりもはるかに凌ぐことができます。さきほど「Googleの量子コンピュータはこのタスクを約3分で完了」と表記しましたがこれは量子コンピュータが得意なタスクの計算を行ったものです。これは特定のタスクにおいて従来のコンピュータよりも圧倒的に高速であることが示されただけですが、量子コンピュータの量子優位性の証拠として注目されています。
量子コンピュータの得意とするところは多数のなかから最適解を見つけるところに威力を発揮します。
単純な計算では現在の古典的とよばれるコンピュータの方がはるかに速いです。量子コンピュータは古典的コンピュータの置き換わりをするのものではなくて、それぞれの得意部分を補って連携していくものです。
量子コンピュータの特性
量子コンピュータはいくつかの特性により得意分野があり、その性能が発揮されます。
量子並列性
量子ビットは重ね合わせ状態を持つことができるため、複数の計算経路を同時に探索できます。これにより、同じ問題を解くために古典コンピュータよりも少ないステップで解答を見つけることができる可能性があります。
量子もつれ
量子ビットは相互作用して量子もつれ状態を形成することができます。これにより、複雑な相関や結びつきを持つ問題を効率的に解決できる可能性があります。
インターフェリング
量子ビットの重ね合わせ状態により、量子アルゴリズムは計算の間に干渉を利用して、望ましい解に対する確率を増加させることができます。
代表的な量子アルゴリズムと用途
| アルゴリズム | 用途 | 内容 |
| ショアの因数分解アルゴリズム | 暗号解読 | 大数の素因数分解を高速に実行 |
| グローバーの探索アルゴリズム | オラクル検索問題、組み合わせ最適問題 | 構造化されていないデータベースから目的のデータを見つけ出す、最適な組み合わせを見つける |
| HHL線形ソルバー | 線形方程式の解法 | 大規模な線形方程式を効率的に解く |
| 量子シミュレーションアルゴリズム | 量子化学、材料科学 | 分子や材料などの量子系の振る舞いをシミュレーション |
| 量子最適化アルゴリズム | 物流最適化、金融ポートフォリオ最適化 | 複雑な最適化問題を効率的に解く |
| 量子機械学習アルゴリズム | 画像認識、音声認識、自然言語処理 | 機械学習の精度向上 |
| 量子モンテカルロ法 | 物理学、化学 | 量子系を統計的にシミュレーション |
| 量子アニーリング | 最適化問題 | 組み合わせ最適問題を解く |
| 量子ニューロラルネットワーク | 画像認識、音声認識、自然言語処理 | 量子力学に基づいてニューラルネットワークを構築 |
| 量子近似最適解アルゴリズム | 組合せ最適化問題 | 従来のアルゴリズムよりも高精度な近似解を効率的に求める |
| 量子推薦システム | 商品推薦、情報推薦 | 量子力学に基づいて、ユーザーに最適な商品や情報を推薦 |
代表的な量子アルゴリズムには、ショアの素因数分解アルゴリズム、グローバーの探索アルゴリズムなどがあります。これらのアルゴリズムは、特定の問題を解決するために量子コンピュータが有効であることを示しています。量子コンピュータの得意な計算は多くの選択候補のなかから一つの良い答えを見つけることです。
ただし、得意なことはわかっていてもそれを量子コンピュータのアルゴリズムで記述することは現時点では容易ではありません。正しい解を見つけるためには、その課題に対応する量子回路を構築し、量子干渉というテクニックをどのように適用させるかは、人間が考える量子アルゴリズムです。
そうです、量子コンピュータはただの量子ビットやその他の量子回路にすぎません。量子コンピュータが得意な課題を人間が見つけてそれを量子アルゴリズムで動かして答えを得ています。効果的に解決できるようになるにはまだ時間がかかる可能性があります。
量子コンピュータが貢献できる主な具体的な分野は、材料開発、金融、物流最適化、医薬品開発、機械学習がありますが、現在の実用化レベルは、まだ研究開発段階です。
現在の量子コンピュータはどこまで進んでいるか?
量子コンピュータのハードウェアは最初に言いましたように巨大な金属の容器に入っています。これは主に冷却装置であり、量子ビットのチップ、量子ゲートを極低温にするためのものです。では、実際に量子ビット自体の数は現在どこまで進んでいるでしょうか?
Google の新しい量子コンピュータは、Sycamore 量子プロセッサは70量子ビットです。
IBMの量子コンピュータでは、
2021年 Eagle 127量子ビット
2022年 Osprey 433量子ビット
2023年 Condor 1121量子ビット
のように毎年順調に量子ビット数を増やしています。Condorと同時にエラー率を大きく改善した133量子ビットのHeronも発表されました。
量子ビット数
2023年5月21日 IBM、東京大学、シカゴ大学は10万量子ビットを搭載した量子を中心としたスーパーコンピュータの開発に向けて今後10年間で1億ドルの投資を伴う取り組みについて発表しています。今後10年で飛躍的な発展とブレークスルーが起こるかもしれません。
さて、IBMの量子コンピュータで量子ビットの数がなぜに127,433,1121のように中途半端な数で奇数になるのでしょうか?
もっときりのいい数字(今のコンピュータでの2の倍数や馴染みのある32ビットとか64ビットとか16の倍数)ではないのか、それは量子ビットと量子ゲートの物理的な制約や設計上の要因によるものです。
IBM量子プロセッサの外観
IBM量子プロセッサの量子ビットの配置構造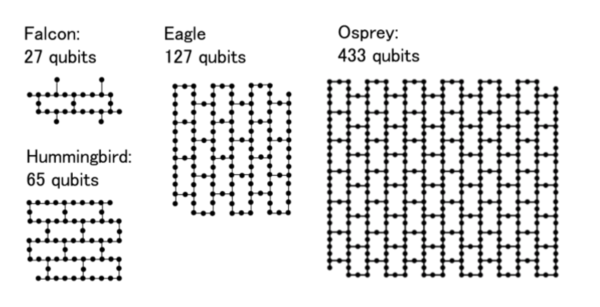
量子ビットは物理的な装置で実装されるため、その配置には特定の制約があります。量子ビットをチップ上に配置する際に、物理的な配線や接続性などの制約が存在し、これが量子ビット数を選択する要因になることがあります。
Eagle:127量子ビットを例にとると各量子ビットは、隣接する2つの量子ビットと接続されています。17個の量子ビットで構成された7つのリングはそれぞれ中央の量子ビットで接続されています。
IBMの127量子ビット・プロセッサ「Eagle」の物理構造
表層下の一層目に量子ビットが連結された層があるのが分かります。
1,000量子ビットを超えるものとして、2023/10にAtom Computingが1,180量子ビットの中性原子プロセッサを発表しました。https://atom-computing.com/quantum-startup-atom-computing-first-to-exceed-1000-qubits/
この量子コンピュータはIBMの超電導方式と違い、冷却原子方式を採用しています。
量子コンピュータの一種である量子アニーリングコンピュータの利用
IBMやGoogleが開発を行っている超電導を使用した冷却された量子コンピュータはまだ実践向きの利用はありません。
量子化学、暗号解読、最適化問題、機械学習への適用はこれからの開発となります。
それに対して量子アニーリングの量子コンピュータではすでに最適化問題での解法がすすんでいます。
例えばデンソーでは工場内を走る自動搬送車の渋滞軽減に活用されています。TDKでは原子レベルの磁性体の最適な組み合わせを量子アニーリングで求めています。
ただし、量子アニーリングは現在のところ特定の最適化問題に特化しており、その他のタイプの問題には適していません。こちらも今後の研究、開発によるところも多いようです。
最後に
今回、量子コンピュータでの計算で重要なエラー訂正の話は省略いたしましたが、量子コンピュータとはどういうもので、それを動かす量子アルゴリズムと量子回路の関係が少しでもお分かりになれば幸いです。
量子コンピュータの中枢である量子ビットの数、量子ゲートの種類は日々拡張されています。10万量子ビットができたら何ができてしまうのか、いろんな事象の課題解決のブレークスルーが起こるかと思います。そのためには量子アルゴリズムももっと容易に作れるようにならないといけません。
この記事をみて量子アルゴリズムに興味を持たれプログラミングをされたい方は、Qiskit や Cirq などの量子コンピュータプログラミング言語がおすすめです。
参考資料
・「すっきり!がってん!量子コンピュータの本」森貴洋著 電気書院
・「量子コンピュータが人工知能を加速する」西森秀稔、大関真之介著 日経BP社
・【特集】量子技術
https://www.jst.go.jp/crds/column/quantum/index.html
・量子セキュリティ・量子ネットワークの技術・産業の国内外動向 JST 研究開発戦略センター
https://www8.cao.go.jp/cstp/ryoshigijutsu/jitsuyo_wg/3kai/sanko6.html
初期費用無料、ドメインが実質0円(年間最大3,882円お得)になる
サーバーセット割特典を展開中です。

※ユーザーノートの記事は、弊社サービスをご利用のお客様に執筆いただいております。
医療メーカーで新素材研究開発後、電機メーカーで制御器系システム開発を経てIT系マルチエンジニアをしています。またデザイン思考を実践し、アート思考などのいろんな思考方法に興味があります。






 目次へ
目次へ